Mountain Car

Handling sparse reward challenges in reinforcement learning using DQN and Dyna-Q algorithms

Technical Report Code

The Mountain Car environment presents a classic reinforcement learning challenge where an agent must learn to drive a car up a steep hill by building momentum through strategic back-and-forth movements. The sparse reward structure (only -1 per timestep with no intermediate feedback) makes this seemingly simple task surprisingly difficult for standard RL algorithms. We explored both model-free (DQN with auxiliary rewards) and model-based (Dyna-Q) approaches to overcome this challenge.

Top: The Mountain Car environment with the car starting at the bottom of the valley. Bottom: Episode duration when playing randomly - the agent never succeeds and always hits the 200 timestep limit.

Methods

Deep Q-Learning (DQN)

We implemented the standard DQN$^{[1]}$ algorithm with experience replay and target networks. The Q-learning update rule with neural networks is:

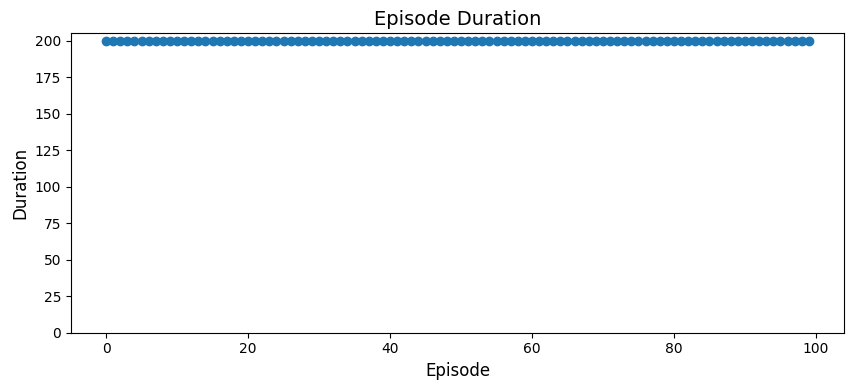
\[Q_{\theta}(s, a) \leftarrow Q_{\theta}(s, a) + \alpha \left[ r + \gamma \max_{a'} Q_{\hat{\theta}}(s', a') - Q_{\theta}(s, a) \right]\]

However, vanilla DQN struggled with the sparse rewards, failing to complete the task even after 1000 episodes despite the loss function converging.

Auxiliary Reward Functions

To address the sparse reward problem, we experimented with two approaches:

1. Heuristic Reward Function: We designed a domain-specific reward that incentivizes both position and velocity:

\[r_{aux} = |s'_p - s_{p_0}| + \frac{|s'_v|}{2 \times s'_{v_{max}}}\]

2. Random Network Distillation (RND): An environment-agnostic approach that encourages exploration by using the prediction error between a fixed random network and a learned predictor network as intrinsic reward.

Dyna-Q

We also implemented Dyna-Q$^{[2]}$, which combines model-free and model-based learning by using a learned environment model to generate simulated experiences. Since Mountain Car has continuous states, we discretized the state space using different bin sizes (small, medium, large) to study the effect of state resolution on learning.

Results

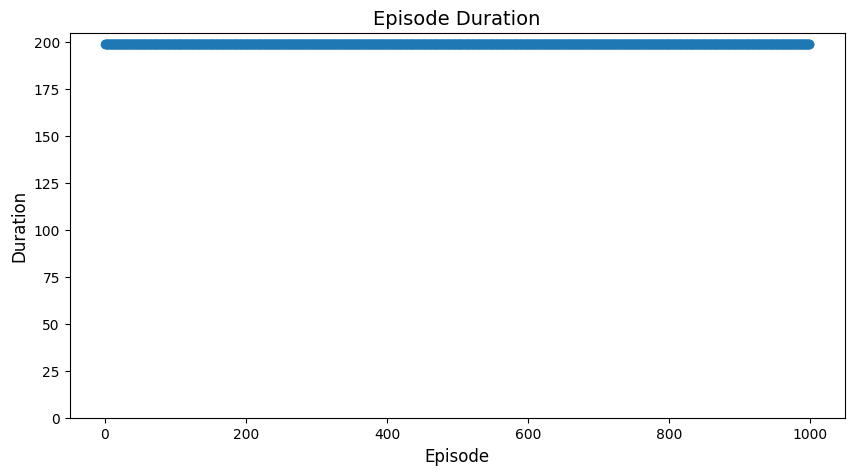
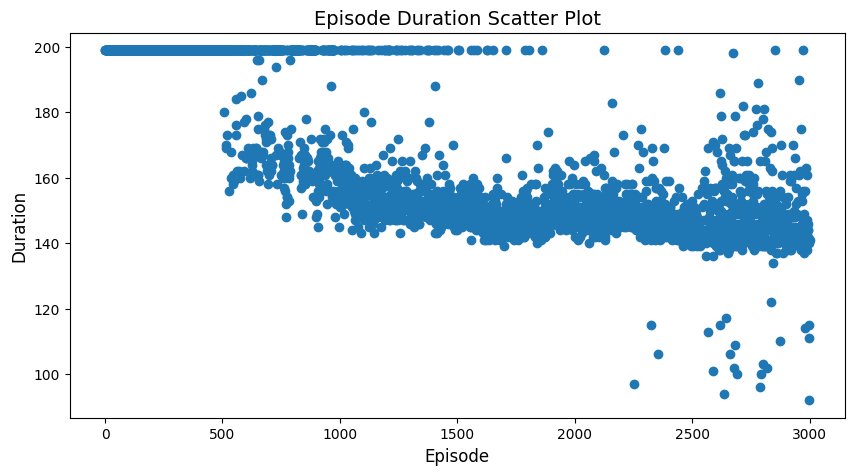
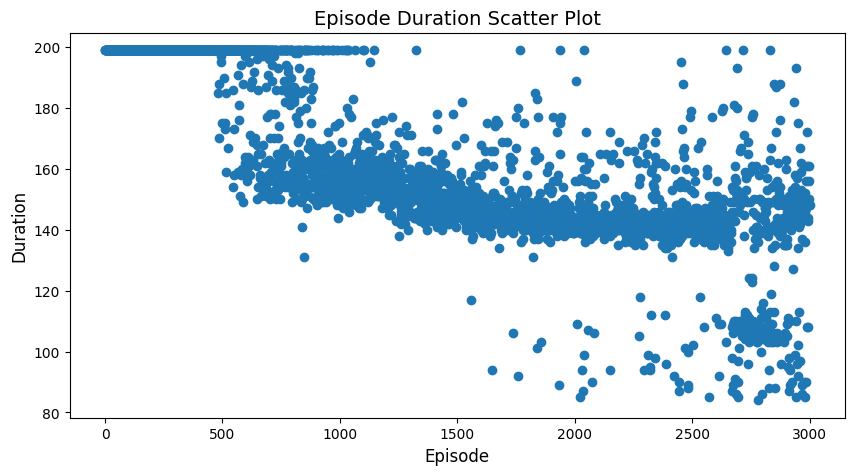
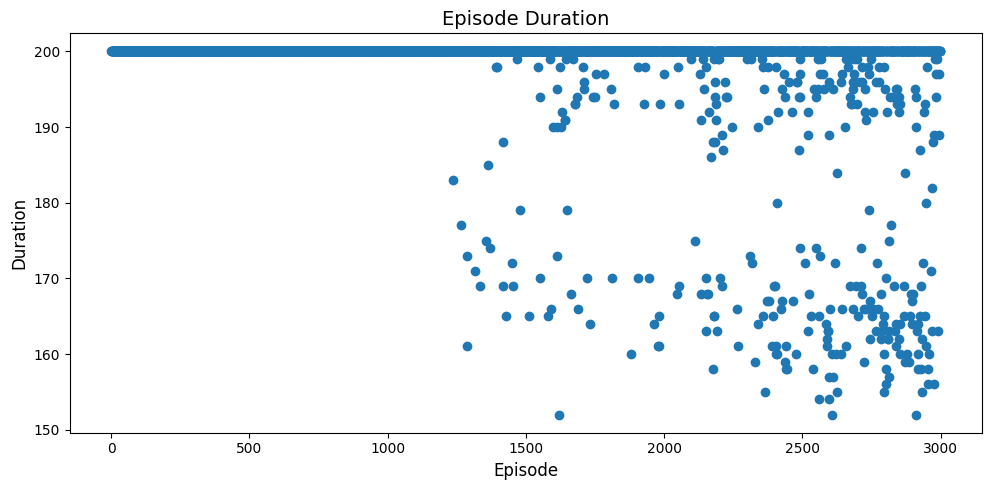
We report the episode duration over training for each method below. Lower value means the model has learned to finish the task faster.
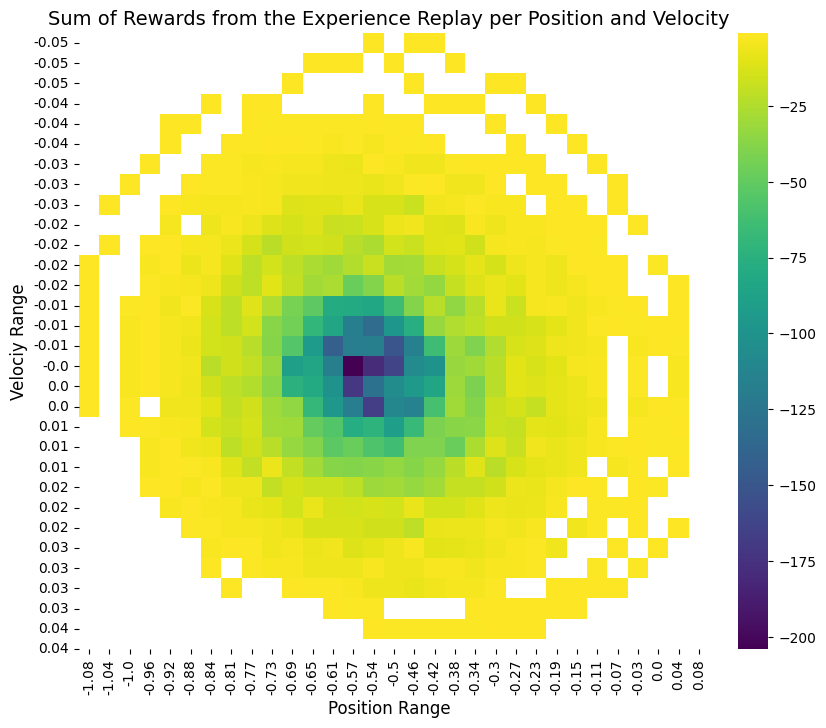
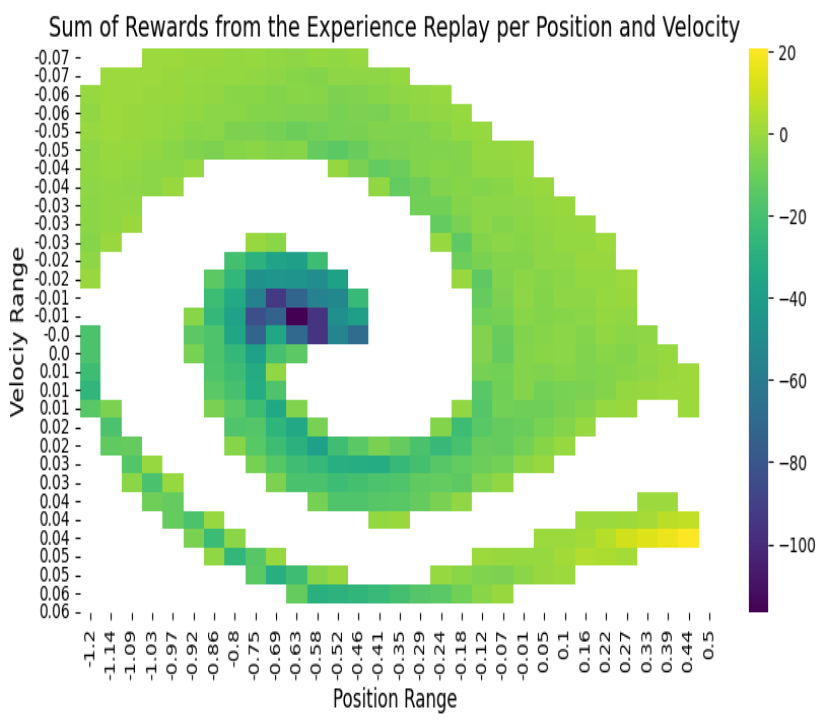
Episode duration over training for different algorithms for: (1) Vanilla DQN, (2) DQN with heuristic reward, (3) DQN with RND, (4) Dyna-Q. Lower duration indicates successful task completion. Both auxiliary reward methods help DQN learn, with RND achieving success slightly earlier (~500 episodes) than the heuristic reward (~600 episodes).

Reward Distribution Analysis

One fascinating insight comes from visualizing where each algorithm accumulates rewards in the state space. For each of the 4 methods, we report the sum of reward per position and velocity. Position=0.5 is the final state.
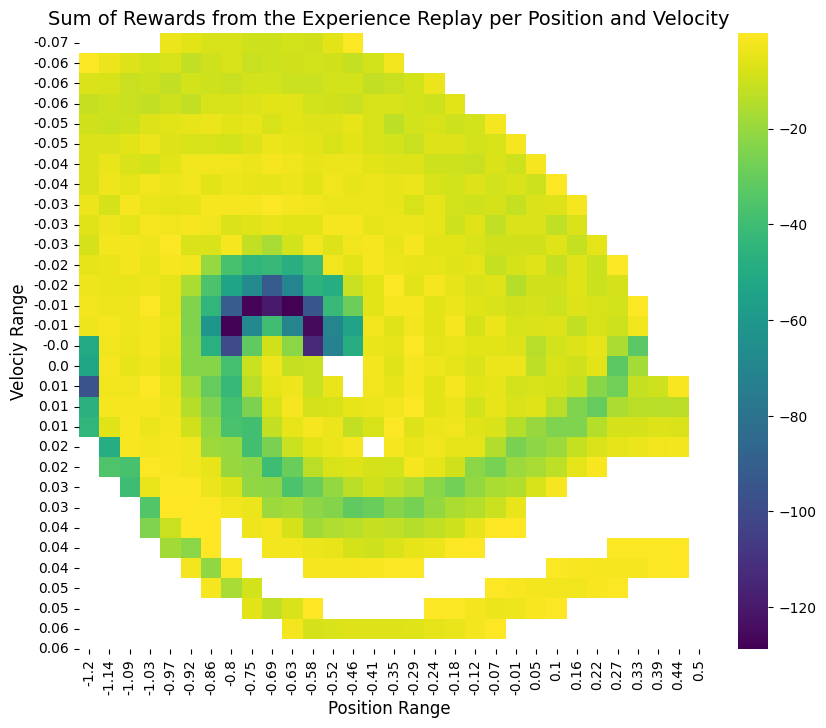
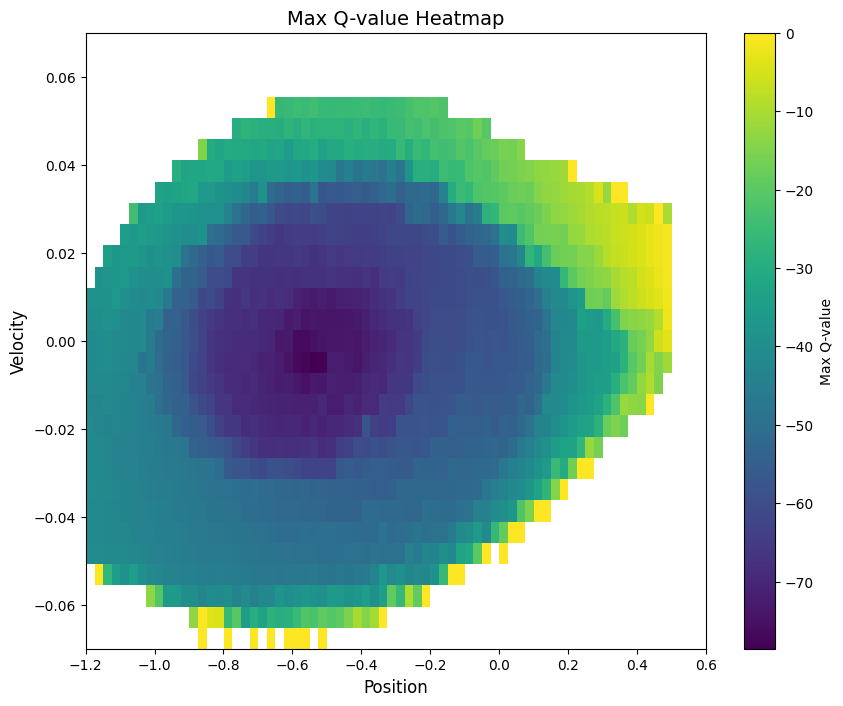
Heatmaps showing the sum of rewards at each state (position vs velocity) from the last 10k experiences. The heuristic reward creates a clear gradient leading to the goal, while RND explores more broadly across the state space.

Key Findings

  1. Sparse rewards are challenging: Vanilla DQN completely fails without auxiliary rewards, highlighting the importance of reward shaping or intrinsic motivation in sparse reward environments.

  2. RND vs Heuristic rewards: While both approaches succeed, RND learns slightly faster and is more generalizable since it doesn’t require domain knowledge. The heuristic reward creates more interpretable learning patterns focused on reaching the goal.

  3. Discretization matters: For Dyna-Q, medium-sized bins provided the best balance between state resolution and learning speed. Too large bins lose important dynamics, while too small bins slow learning.

  4. Multiple policies emerge: Interestingly, all successful agents learned to complete the task in approximately two distinct durations (~90 or ~150 steps), suggesting multiple valid strategies for solving the Mountain Car problem.

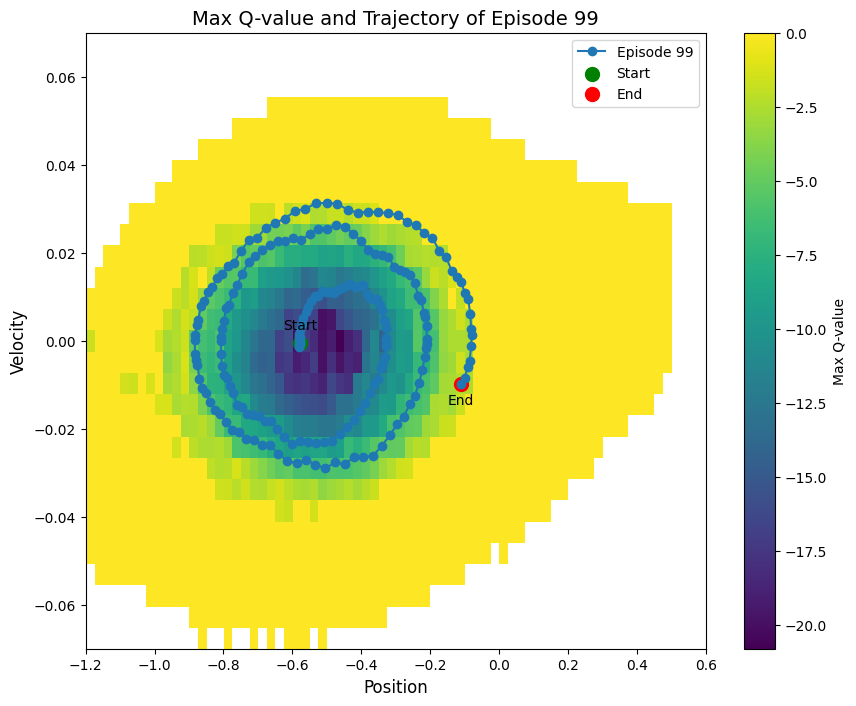
Below is how the model learns to achieve the task during traning at the episodes 99, 499, and 2998:
Evolution of Dyna-Q's exploration over training, showing how the agent progressively discovers more of the state space and refines its policy.

References

  1. Deep Q-Learning: Volodymyr Mnih and Koray Kavukcuoglu and David Silver and Alex Graves and Ioannis Antonoglou and Daan Wierstra and Martin Riedmiller (2013). Playing Atari with Deep Reinforcement Learning. arXiv preprint arXiv:1312.5602. https://arxiv.org/abs/1312.5602

  2. Dyna-Q: Baolin Peng and Xiujun Li and Jianfeng Gao and Jingjing Liu and Kam-Fai Wong and Shang-Yu Su (2018). Deep Dyna-Q: Integrating Planning for Task-Completion Dialogue Policy Learning. arXiv preprint arXiv:1801.06176. https://arxiv.org/abs/1801.06176